Regressão de Descontinuidade (RDD)
- Fernanda Kelly
- 12 de ago. de 2025
- 13 min de leitura
Imaginem uma novela estatística (e um tanto economista também)... Temos dois personagens principais:
Regressão de Descontiunidade (RD)
Diferenças em Diferenças (Diff-in-Dif ou DiD para os mais íntimos)
Elas não são rivais, são primas que adoram analisar políticas públicas, mas cada uma tem o seu jeitinho peculiar de fazer comparações.
O que é Regressão de Descontinuidade (RD)?
Vamos exemplificar para o melhor entendimento de todes:
O governo dá uma bolsa para alunos que tiram nota maior ou igual a 7. Quem tirou 6.9 ficou de fora do programa e quem tirou 7.1 passou a fazer parte do programa.Agora suponha que é de interesse saber se essa bolsa fez diferença na média das notas do semestre seguinte. Aí vem a RD e diz:
"Vamos comparar alunos quase idênticos: um que tirou 6.9 e outro 7.0. Eles são parecidos em tudo, exceto por esse pontinho de corte mágico que define quem ganha e quem não ganha a bolsa do programa. E se tiver uma "quebra" no gráfico ali no 7.0... AHA! Talvez seja o efeito da bolsa.A Regressão de Descontinuidade é isso: aproveita uma regra com corte fixo (threshold) para estimar um efeito causal quase como num experimento natural.
E o Diferenças em Diferenças (DiD)?
Vamos imaginar outro enredo com o seguinte exemplo:
Dois estados. Um aprovou uma política pública, o outro não. Você tem dados antes e depois dessa mudança.Aí que chega o tal do DiD e um economista que adora gráfico de linha, e diz:
"Vamos ver o que aconteceu nos dois grupos com o tempo. Se ambos estavam caminhando parecido antes, e depois da política só um grupo muda o rumo, provavelmente foi por consequência da política aplicada."Ou seja, o DiD compara a evolução temporal de dois grupos, e estima o efeito da política como a diferença entre as diferenças. É tipo estudos de caso controle na saúde, conhece? Só que aqui temos a questão temporal. Mas, agora você deve estar se perguntando:
E se a gente juntar RD + DiD?
Agora sim: A Regressão de Descontinuidade com Diferenças em Diferenças é o combinado S-U-P-R-E-M-O, mas isso não quer dizer que ele seja fácil, tá? Vamos por partes.
A ideia até o momento foi trazer que há dois métodos MUITO usados nesses casos de comparações entre um ponto de corte e seu antes e depois e que há diferença entre eles. Tudo isso foi para nos qualificar e entender onde e qual hipótese podemos atender em ambos os métodos. Logo, com o intuito de aprendizagem, vamos aprofundar no primeiro método, a Regressão de Descontinuidade (RD) e, para isso, sempre vou trazer exemplos didáticos e, as vezes, exemplos no R para você acompanhar.
Vamos juntes?
Em um esforço para lidar com os problemas sociais e de saúde pública associados ao consumo de álcool por menores de idade, um grupo de presidentes de universidades americanas fez lobby junto aos estados para que o limite mínimo legal de idade para consumir álcool retorne ao limiar da era do Vietnã, que era de 18 anos.
A teoria por trás desse esforço é que permitir o consumo legal de álcool a partir dos 18 anos desencoraja o consumo excessivo e promove uma cultura de consumo maduro de bebidas alcoólicas. Isso contrasta com a visão tradicional de que o o limite legal de 21 anos, embora uma ferramenta direta e imperfeita, reduz o acesso dos jovens ao álcool, prevenindo assim alguns danos. E você deve estar se perguntando qual seria a hipótese dessa grande movimentação e, lá vem ela:
Qual o impacto de ter idade para beber álcool sobre o número de mortes no trânsito?
É uma questão de grande valia para qualquer país, incluindo o nosso Brasilzão, mas a título de exemplo, vamos pensar nesse caso dos EUA.
Vamos instalar alguns pacotes?
Bora lá:
install.packages(rdrobust)
install.packages(sjPlot)
install.packages(readr)
install.packages(broom)
install.packages(estimatr)E se você quiser me acompanhar nos resultados, vamos plantar uma sementinha:
set.seed(42)E cadê a base de dados?
Para o download do banco de dados, utilize o seguinte código na sua linha de comando no RStudio:
mlda_df <- readr::read_csv("https://raw.githubusercontent.com/seramirezruiz/stats-ii-lab/master/Session%206/data/mlda.csv")A estrutura da base de dados e suas variáveis escolhidas para esse exemplo se encontra abaixo.
mlda_dfBase <- mlda_df %>%
dplyr::select(outcome, agecell, treatment, forcing)
E porquê escolhi essas variáveis?
Na base de dados exposta, a variável outcome é o número de mortes no trânsito por 100 mil habitantes, agecell é a faixa de idade, treatment indica que a faixa é maior do que 21 anos (1 e 0 c.c.) e forcing é a variável padronizada a fim de 21 anos ser equivalente a zero e a variação se manter entre 2 e menos 2, sendo essa a variável de atribuição. Podemos imaginar que a variável D (treatment) define o recebimento ou não do tratamento, de modo que:
D = 1 se X >= c
D = 0 se X < c
Em que X é a variável de atribuição e c é o ponto de corte. A RDD é a baseada em uma hipótese:
Todos os outros fatores (que não D) estão evoluindo de maneira suave em torno de c.
É possível supor que o comportamento dos indivíduos entre 19 e 23 anos não sofre grandes alterações, devido a proximidade da idade, de modo que atendemos as hipóteses necessárias. O segundo passo é determinar qual designer de modelagem utilizaríamos quando c seja claro ou não. Para este método RDD, se um ponto específico marca o corte e nada antes dele receba o tratamento e todos depois dele recebam, teremos um modelo sharp. Caso a linha de corte não seja clara, ou seja, existam indivíduos que recebem e não recebem o tratamento na mesma etapa, teremos um modelo fuzzy.
Já começou a palhaçada, né?
Sim! Temos dois métodos de analisar dados com o RDD:
sharp: O ponto de corte determina exatamente quem recebe e quem não recebe o tratamento.
fuzzy: O ponto de corte aumenta a probabilidade de receber o tratamento, mas não garante.
Graficamente,

Vamos visualizar qual é o método adequado para os nossos dados?
O primeiro passo é avaliar se aplicaremos uma RDD do tipo sharp ou do tipo fuzzy. No caso, o corte na lei é claro, legalizando o consumo de álcool no momento em que o indivíduo completou 21 anos.
ggplot(mlda_dfBase, aes(x = agecell,y = treatment,color = factor(treatment))) +
geom_point(size = 1.5, alpha = 0.5,position = position_jitter(width = 0, height = 0.25, seed = 1234)) +
labs(x = "Idade",y = "Probabilidade de ser tratado") + scale_color_discrete(name = " ",labels = c("Não possui idade legal para beber", "Possui idade legal para beber")) +
geom_vline(xintercept = 21, linetype = "dotted") +
theme_bw() +
theme(legend.position = "bottom")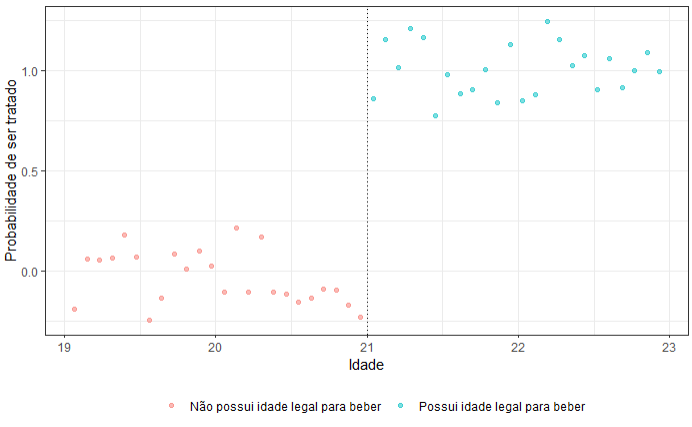
Sendo assim, através do plot ao lado, podemos observar e já indicar que o uso de uma RDD sharp é o indicado. A partir disso, analisaremos então o comportamento dos dados com o objetivo de entender qual modelo melhor capturará a variação dos dados.
Para fins didáticos, inicialmente vamos assumir que a relação entre X e Y seja linear e assim, podemos estimar a relação entre o efeito do tratamento por meio da seguinte regressão linear.
Y = alpha + D_tau + betaX + epsilon
Se todos os fatores variam suavemente de acordo com X, então beta seria uma boa estimativa do valor de X para quem está acima da linha de corte e alpha para aqueles abaixo da linha de corte, de modo que o efeito causal seria dado por betaX - alpha. Para supormos isso, é necessário que todos os fatores que afetam Y variem suavemente com X. Caso isso não se confirme, tau será estimado com viés.
Observe que a variável forcing ou running variable é centralizada em 0 (idade 21) e representa a distância em anos a partir dos 21 anos, enquanto o treatment (0 menor que 21 anos e 1 maior/igual que 21 anos) é apenas binário, acima/abaixo de 21 anos. Assim, primeiramente, iremos modelar os dados utilizando um modelo linear com retas comuns.
linear_common_slope <- stats::lm(outcome ~ treatment + forcing, data = mlda_dfBase)
linear_common_slope %>%
sjPlot::tab_model()
Uma das suposições do modelo de regressão linear é a homoscedasticidade dos resíduos e, a partir do gráfico abaixo, podemos observar que os resíduos estão distribuídos de uma forma aleatória. fazendo com que o nosso modelo, até o momento, passe nesse critério de avaliação.
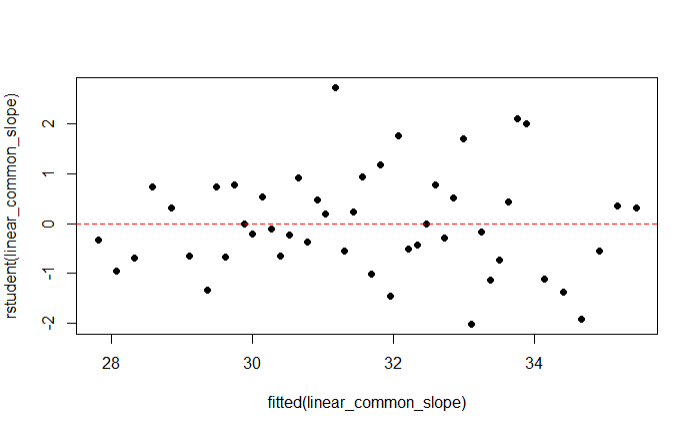
plot(rstudent(linear_common_slope) ~ fitted(linear_common_slope), pch = 19)
abline(h = 0, lty = 2, col = "red")Em relação a normalidade dos resíduos, a imagem abaixo indica que há normalidade, mas podemos testar com testes não paramétricos essa suposição. O teste que iremos utilizar se chama Teste de Shapiro Wilk.

hist(x = linear_common_slope$residuals, col = 'gray',
xlab = 'Resíduos',
ylab = 'Densidade de Probabilidade',
probability = TRUE)
lines(density(linear_common_slope$residuals))E de acordo com o teste, podemos não rejeitar a hipótese de que os resíduos do modelos são distribuídos normalmente ao nível de 95% de significância.
stats::shapiro.test(linear_common_slope$residuals)
Shapiro-Wilk normality test
data: linear_common_slope$residuals
W = 0.9817, p-value = 0.6508De acordo com nossas suposições para modelos lineares com inclinação comum, consideramos que o efeito do tratamento não depende da variável forcing. Uma forma de visualizar os resultados da modelagem é com a imagem abaixo.

Portanto, podemos afirmar que, com base em nosso beta_{1}, podemos esperar 4,53 mortes adicionais por acidentes de trânsito a cada 100.000 habitantes para aqueles que podem consumir legalmente bebidas alcoólicas. Também podemos observar que, para cada ano de aumento na idade, o número de mortes por 1000.000 habitantes diminui em 3,15.
E você deve estar se perguntando:
Fê, isso aí é uma regressão "normal". Faço isso todo santo dia e você me diz que a RDD é isso?
É isso, mas a RDD não quer explicar toda a relação entre X e Y, e sim o salto no resultado exatamente no ponto de corte c. Veja a imagem abaixo:

Agora, por exemplo, reestimaremos essa regressão permitindo que haja variação entre as retas da regressão. Isso pode ser feito através da introdução de um termo interativo no modelo. O intercepto é o nível médio abaixo do corte, tratamento é diferença de nível no corte (o “salto”), X é a inclinação abaixo do corte e tratamento:X é diferença de inclinação acima do corte.

linear_different_slope <- lm(outcome ~ treatment*forcing, data = mlda_df)
linear_different_slope %>%
sjPlot::tab_model()O modelo se adequou um pouco melhor aos dados, com um r_quadrado de 0.722, sendo 0.019 maior que o modelo anterior com retas comuns.

Portanto, podemos afirmar que, dado beta_{1}, podemos esperar 4,53 mortes adicionais por acidentes de veículos a cada 100.000 pessoas para aqueles que podem legalmente consumir bebidas alcoólicas no limite de idade. Agora temos duas inclinações diferentes para mudanças na idade. Para indivíduos com menos de 21 anos, um aumento de um ano na idade resultaria, em média, 2,57 mortes a menos por acidentes de veículos. Para aqueles que têm idade legal para beber, esperaríamos 3,73 (- 2,57 + (-1,16) ) mortes a menos por 100.000 pessoas para aumento de um ano de idade.
Podemos também deixar o treatment (D) variar ao longo da variável forcing (X), respeitando as premissas de modelos não lineares. Assim, os efeitos do tratamento D_{i} podem variar ao longo da variável X_{i}. No caso, estimaremos um modelo com interações quadráticas.
quadratic <- lm(outcome ~ forcing +
I(forcing^2) +
treatment +
I(forcing * treatment) +
I((forcing^2) * treatment),
data = mlda_df)
# quadratic %>%
# generics::tidy() %>%
# sjPlot::tab_df()
Logo, podemos dizer que, considerando nosso tau, podemos esperar 4,66 mortes adicionais por acidentes de veículos a cada 100.000 pessoas para aqueles que podem legalmente consumir bebidas alcoólicas no limite de idade. Também poderíamos calcular o valor esperado de Y em diferentes níveis de X. Digamos que queiramos saber qual é o valor esperado para pessoas de 23 anos. Como nossa variável de forçamento é 0 aos 21 anos de idade, podemos considerar 23 como 2. Além disso, pessoas de 23 anos estão acima da idade legal mínima para beber, portanto, para elas, o valor de D é 1.
E(Y_{i}|X = 2, D = 1) = 29.8 - 2.93(2) - 0.19(2)^2+4.66(1) - 0.82(2.1) + 0.2(2.1) = 27.01
Com base nisso, esperaríamos uma taxa de mortalidade por acidentes de veículos de 27,01 a cada 100.000 pessoas para pessoas de 23 anos. O gráfico da modelagem quadrática (não linear) se encontra a seguir.

E como se calcula o efeito?
Para essa tarefa vamos utilizar o pacote rdrobust. A função rdrobust realiza regressões locais para ambos os lados do ponto de corte utilizando o cálculo da largura de banda ideal.
Não se preocupe que vou lhe ensinar, tá?
Como falei anteriormente, podemos calcular o efeito médio causal local (Local Avarage Treatment Effect) para aqueles com mais de 21 anos por meio de uma estimação dos pontos por meio de um regressão polinomial local com correção de viés.
library(rdrobust)
llr <- rdrobust::rdrobust(mlda_df$outcome, mlda_df$forcing,
c = 0,
kernel = "tri",
bwselect = "mserd")
summary(llr)Como resultado,
Sharp RD estimates using local polynomial regression.
Number of Obs. 48
BW type mserd
Kernel Triangular
VCE method NN
Number of Obs. 24 24
Eff. Number of Obs. 6 6
Order est. (p) 1 1
Order bias (q) 2 2
BW est. (h) 0.487 0.487
BW bias (b) 0.738 0.738
rho (h/b) 0.660 0.660
Unique Obs. 24 24
=============================================================
Point Robust Inference
Estimate z P>|z| [ 95% C.I. ]
-------------------------------------------------------------------- RD Effect 4.901 1.881 0.060 [-0.198 , 9.674] =============================================================Em linhas gerais, essa saída nos diz que estamos usando o modelo Sharp RD, ou seja, o tratamento muda com certeza após o ponto de corte, que a base de dados possui 48 observações, a BW type mserd utilizada foi escolhida para minimizar o erro quadrático médio do efeito RS, o kernel utilizado foi o triangular, que dá mais peso aos dados próximos do ponto de corte e o VCE method igual a NN é a estimativa da variância feita com o método de vizinho mais próximo (Nearest Neighbor).
Tá, mas o que são esses parâmetros na modelagem?
Se você prestou atenção (mas ATENÇÃO mesmo), você viu que há 3 parâmetros em nossa equação de modelagem: c, kernel e bwselect. O c é o parâmetro que normalmente representa o ponto de corte (cutoff), ou seja, c é o “marco zero” onde a gente olha para os dois lados e vê se há um salto no resultado. É o valor que separa tratados de não tratados, por exemplo.
Quer dizer que tem outros parâmetros?
Sim! Há vários outros, mas vamos por pequenos passos e dar prioridade ao que nos faz engatinhar na modelagem de interesse.
O kernel, por exemplo, é muito utilizado em vários métodos de Inteligência Artificial e há V-Á-R-I-O-S tipos de kernel. No nosso caso, o kernel Kernel triangular é o padrão no rdrobust. Este kernel dá mais peso para observações mais próximas do ponto de corte (margem = 0), implicando melhora na eficiência da estimativa quando o modelo é local.
Vamos visualizar graficamente o que esse kernel triangular está fazendo no RD?
A ideia é bem simples: ele atribui peso máximo às observações exatamente no ponto de corte e vai diminuindo linearmente esse peso conforme a observação se afasta, até chegar a peso zero na extremidade da largura de banda.

O eixo x é a distância da observação até o ponto de corte (em unidades da running variable).
O eixo y é o peso que aquela observação recebe no cálculo da regressão local.
Observações no corte (0) recebem peso máximo (= 1).
À medida que se afastam, o peso cai linearmente até chegar a 0 no limite da largura de banda.
E o que é o parâmetro bwselect?
O bwselect (bandwidth selection) é a estratégia de escolha da largura de banda usada no estimador local (como no local polynomial regression, por exemplo). As opções mais comuns desse parâmetro são:
mserd: um seletor comum de largura de banda ótima para MSE para o estimador do efeito do tratamento RD.
msetwo: dois seletores diferentes de largura de banda ótima para MSE (abaixo e acima do ponto de corte) para o estimador do efeito do tratamento RD.
msesum: um seletor comum de largura de banda ótima para MSE para a soma das estimativas de regressão (em oposição à diferença entre elas).
msecomb1: para min(mserd,msesum).
msecomb2: para median(msetwo,mserd,msesum), para cada lado do ponto de corte separadamente.
cerrd: um seletor comum de largura de banda ótima para CER para o estimador do efeito do tratamento RD.
certwo: dois seletores diferentes de largura de banda ótima para CER (abaixo e acima do ponto de corte) para o estimador do efeito do tratamento RD.
cersum: um seletor comum de largura de banda ótima para CER para a soma das estimativas de regressão (em oposição à diferença entre elas).
cercomb1: para min(cerrd,cersum).
cercomb2: para median(certwo,cerrd,cersum), para cada lado do corte separadamente.
Atente-se que o MSE é o Erro Quadrático Médio e CER é a Taxa de Erro de Cobertura. O padrão da modelagem caso este parâmetro não seja setado, é bwselect = mserd, que foi o que nós usamos.
Para que esse estimador local funcione bem, há a necessidade de controlar as bandas chamadas por h, b e rho.
As opções de largura de banda (h) controla o quão "largamente" o algoritmo olha ao redor de um ponto x para fazer a estimativa. Tipo quando estamos usando o algoritmo k-means e temos que dar parâmetro se ele vai "varrer" os pontos pelo vizinho mais próximo, mais longe ou centroides. Mas, é claro que para tudo há uma consequência:
Uma banda muito pequena -> mais sensível a ruídos (alta variância)
Uma banda muito larga -> mais suavizado (alto viés)
Logo, no contexto de estimação local com intervalos de confiança robustos, h é utilizada para estimar a função, b é a largura do estimador de variância robusta (bias=corretion) e rho a razão entre h e b, ou seja: rho = h/b.
E como funciona isso?
Se você não especificar rho, o algoritmo calcula h e b automaticamente, usando a opção de bwselect que você definir. Se você especificar rho, ele só estima h e depois define b. Visualmente,

Logo, com essa explicação meio por cima dos parâmetros que utilizamos, os resultados da nossa modelagem apontam para um efeito não significante, ao nível de 95% de significância, do tratamento para aqueles com mais de 21 anos. E claro, observe que o 0 pertence ao intervalo de confiança, reforçando a conclusão de não significância. MAS, se fosse significativo, diríamos que o efeito estimado seria de 4.90 mortes a mais por 100.000 pessoas com mais de 21 anos.
=============================================================
Point Robust Inference
Estimate z P>|z| [ 95% C.I. ]
-------------------------------------------------------------------- RD Effect 4.901 1.881 0.060 [-0.198 , 9.674] =============================================================Podemos plotar esses resultados da seguinte forma:
rdplot(mlda_df$outcome,
mlda_df$forcing,
c = 0,
kernel = "tri",
title = "Morte em acidentes no transito",
x.label = "Idade a partir de 21",
y.label = "Morte em acidentes no transito (per 100,000)")
Diante de todo o processo que fizemos com a regressão, aqui também podemos modelar de forma quadrática com a função rdrobust(). Nesse caso, o parâmetro p especifica a ordem do polinômio local que queremos para construir o estimador pontual. O padrão é p = 1 (regressão linear local).
Testa aí e veja se o resultado se altera?
E aproveita e já comenta o seu resultado.
Mas vamos lá...
Esse não é um método muito fácil de entender e aplicar assim de "cara". Foi isso que eu senti, mas, ao mesmo tempo, ele é interessante e consegue auxiliar em muitos casos reais do cotidiano de um Estatístico ou qualquer outro profissional que trabalha com modelagem. A intenção desse post foi trazer mais uma possibilidade de modelar conforme os dados se apresentam.
Sem aquele tanto de transformação, sabe?
Até porquê nem T-U-D-O é Machine Learning.
Spoiler: O próximo post é sobre o Dif-in-Diff ou DiD que é outra modelagem INCRÍVEL.
Fernanda Kelly | Estatística
Referência



Comentários